####################################################################################################

#r# =============================
#r#  Voltage and Current Divider
#r# =============================

#r# This circuit is a fundamental block in electronic that permits to scale a voltage by an
#r# impedance ratio:

#f# circuit_macros('voltage-divider.m4')

#r# The relation between the input and ouput voltage is:
#r#
#r# .. math::
#r#
#r#     \frac{V_{out}}{V_{in}} = \frac{R_2}{R_1 + R_2}
#r#
#r# This equation holds for any impedances like resistance, capacitance, inductance, etc.

####################################################################################################

import PySpice.Logging.Logging as Logging
logger = Logging.setup_logging()

####################################################################################################

from PySpice.Spice.Netlist import Circuit
from PySpice.Unit import *

####################################################################################################

circuit = Circuit('Voltage Divider')

circuit.V('input', 1, circuit.gnd, 10@u_V)
circuit.R(1, 1, 2, 2@u_kΩ)
circuit.R(2, 2, circuit.gnd, 1@u_kΩ)

simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.operating_point()

for node in analysis.nodes.values():
    print('Node {}: {:5.2f} V'.format(str(node), float(node))) # Fixme: format value + unit
#o#

####################################################################################################

#r# Similarly we can build a circuit that scale a current by an impedance ratio:

#f# circuit_macros('current-divider.m4')

#r# The relation between the input and ouput current is:
#r#
#r# .. math::
#r#
#r#     \frac{I_{out}}{I_{in}} = \frac{R_1}{R_1 + R_2}
#r#
#r# Note the role of R1 and R2 is exchanged.
#r#
#r# This equation holds for any impedances like resistance, capacitance, inductance, etc.

####################################################################################################

circuit = Circuit('Current Divider')

circuit.I('input', 1, circuit.gnd, 1@u_A) # Fixme: current value
circuit.R(1, 1, circuit.gnd, 2@u_kΩ)
circuit.R(2, 1, circuit.gnd, 1@u_kΩ)

for resistance in (circuit.R1, circuit.R2):
    resistance.minus.add_current_probe(circuit) # to get positive value

simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.operating_point()

# Fixme: current over resistor
for node in analysis.branches.values():
    print('Node {}: {:5.2f} A'.format(str(node), float(node))) # Fixme: format value + unit
#o#

8.8.3. Voltage and Current Divider¶

This circuit is a fundamental block in electronic that permits to scale a voltage by an impedance ratio:

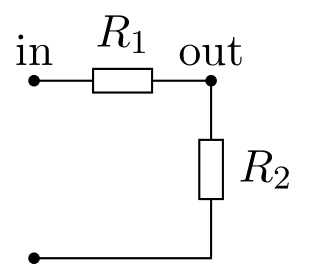
The relation between the input and ouput voltage is:

$\frac{V_{out}}{V_{in}} = \frac{R_2}{R_1 + R_2}$

This equation holds for any impedances like resistance, capacitance, inductance, etc.

import PySpice.Logging.Logging as Logging
logger = Logging.setup_logging()


from PySpice.Spice.Netlist import Circuit
from PySpice.Unit import *


circuit = Circuit('Voltage Divider')

circuit.V('input', 1, circuit.gnd, 10@u_V)
circuit.R(1, 1, 2, 2@u_kΩ)
circuit.R(2, 2, circuit.gnd, 1@u_kΩ)

simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.operating_point()

for node in analysis.nodes.values():
    print('Node {}: {:5.2f} V'.format(str(node), float(node))) # Fixme: format value + unit

Node 2:  3.33 V
Node 1: 10.00 V

Similarly we can build a circuit that scale a current by an impedance ratio:

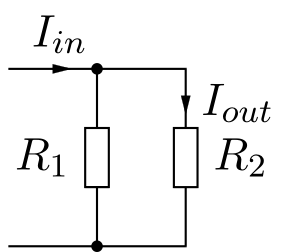
The relation between the input and ouput current is:

$\frac{I_{out}}{I_{in}} = \frac{R_1}{R_1 + R_2}$

Note the role of R1 and R2 is exchanged.

This equation holds for any impedances like resistance, capacitance, inductance, etc.

circuit = Circuit('Current Divider')

circuit.I('input', 1, circuit.gnd, 1@u_A) # Fixme: current value
circuit.R(1, 1, circuit.gnd, 2@u_kΩ)
circuit.R(2, 1, circuit.gnd, 1@u_kΩ)

for resistance in (circuit.R1, circuit.R2):
    resistance.minus.add_current_probe(circuit) # to get positive value

simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.operating_point()

# Fixme: current over resistor
for node in analysis.branches.values():
    print('Node {}: {:5.2f} A'.format(str(node), float(node))) # Fixme: format value + unit

Node vr1_minus:  0.33 A
Node vr2_minus:  0.67 A