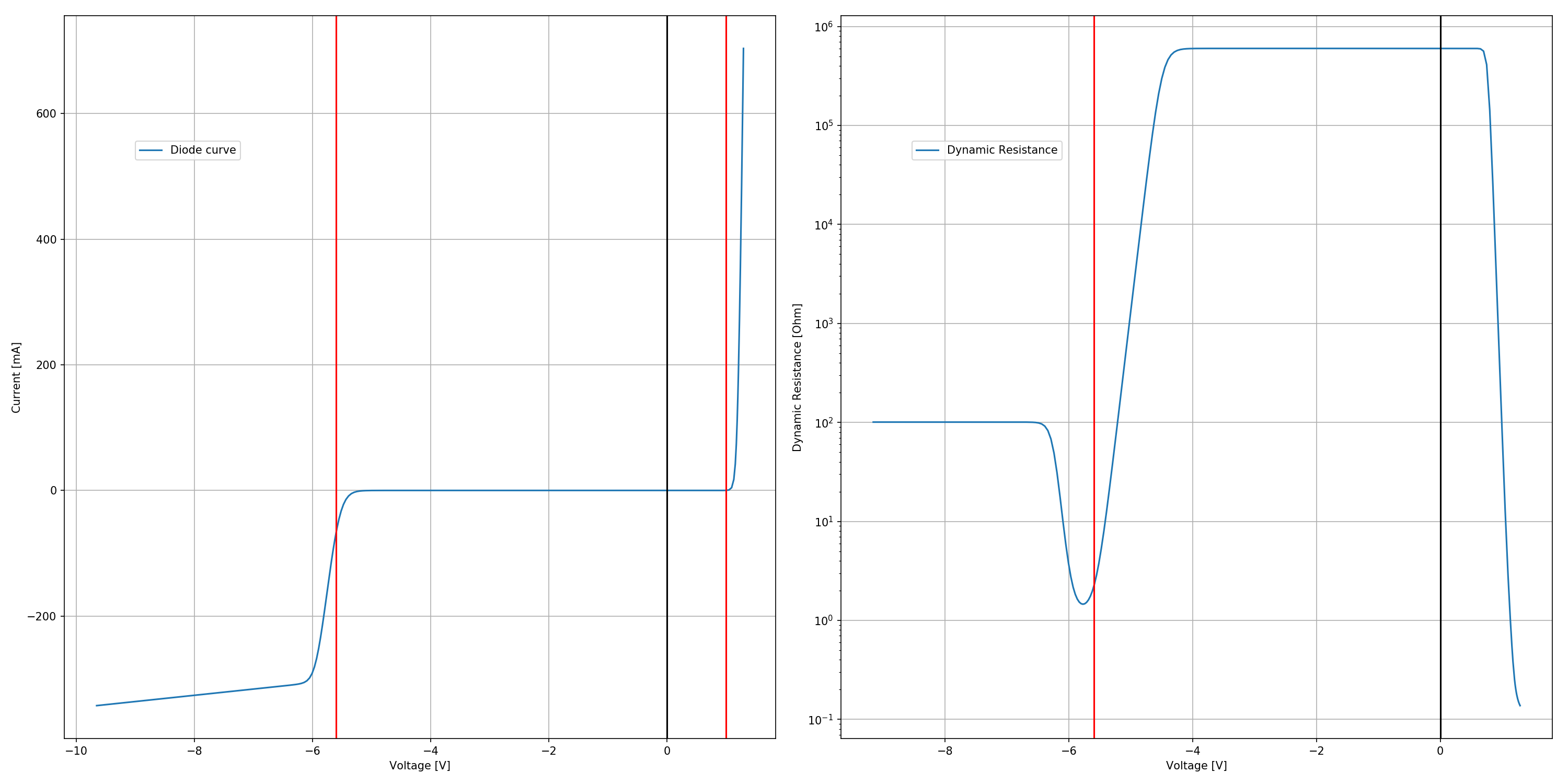
8.4.7. Zener Characteristic Curve¶
- zener-characteristic-curve.py
- zener-characteristic-curve.py
#r# This example shows how to simulate and plot the characteristic curve of a Zener diode.
####################################################################################################
import numpy as np
import matplotlib.pyplot as plt
####################################################################################################
import PySpice.Logging.Logging as Logging
logger = Logging.setup_logging()
####################################################################################################
from PySpice.Doc.ExampleTools import find_libraries
from PySpice.Spice.Netlist import Circuit
from PySpice.Spice.Library import SpiceLibrary
from PySpice.Unit import *
####################################################################################################
libraries_path = find_libraries()
spice_library = SpiceLibrary(libraries_path)
####################################################################################################
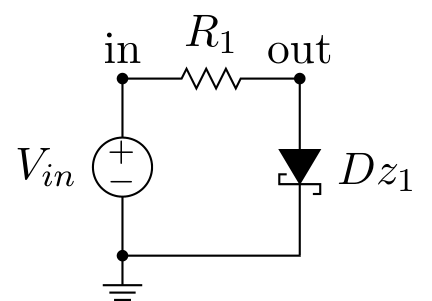
#f# circuit_macros('zener-diode-characteristic-curve-circuit.m4')
circuit = Circuit('Diode DC Curve')
circuit.include(spice_library['1N4148'])
# 1N5919B: 5.6 V, 3.0 W Zener Diode Voltage Regulator
circuit.include(spice_library['d1n5919brl'])
circuit.V('input', 'in', circuit.gnd, 10@u_V)
circuit.R(1, 'in', 'out', 1@u_Ω) # not required for simulation
# circuit.X('D1', '1N4148', 'out', circuit.gnd)
circuit.X('DZ1', 'd1n5919brl', 'out', circuit.gnd)
simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.dc(Vinput=slice(-10, 2, .05)) # 10mV
figure = plt.figure(1, (20, 10))
zener_part = analysis.out <= -5.4@u_V
# compute derivate
# fit linear part
axe = plt.subplot(121)
axe.grid()
# Fixme: scale
axe.plot(analysis.out, -analysis.Vinput*1000)
axe.axvline(x=0, color='black')
axe.axvline(x=-5.6, color='red')
axe.axvline(x=1, color='red')
axe.legend(('Diode curve',), loc=(.1,.8))
axe.set_xlabel('Voltage [V]')
axe.set_ylabel('Current [mA]')
axe = plt.subplot(122)
axe.grid()
# Fixme:
# U = RI R = U/I
dynamic_resistance = np.diff(-analysis.out) / np.diff(analysis.Vinput)
# axe.plot(analysis.out[:-1], dynamic_resistance/1000)
axe.semilogy(analysis.out[10:-1], dynamic_resistance[10:], basey=10)
axe.axvline(x=0, color='black')
axe.axvline(x=-5.6, color='red')
axe.legend(('Dynamic Resistance',), loc=(.1,.8))
axe.set_xlabel('Voltage [V]')
axe.set_ylabel('Dynamic Resistance [Ohm]')
# coefficients = np.polyfit(analysis.out[zener_part], dynamic_resistance[zener_part], deg=1)
# x = np.array((min(analysis.out[zener_part]), max(analysis.out[zener_part])))
# y = coefficients[0]*x + coefficients[1]
# axe.semilogy(x, y, 'red')
plt.tight_layout()
plt.show()
#f# save_figure('figure', 'zener-characteristic-curve.png')
This example shows how to simulate and plot the characteristic curve of a Zener diode.
import numpy as np
import matplotlib.pyplot as plt
import PySpice.Logging.Logging as Logging
logger = Logging.setup_logging()
from PySpice.Doc.ExampleTools import find_libraries
from PySpice.Spice.Netlist import Circuit
from PySpice.Spice.Library import SpiceLibrary
from PySpice.Unit import *
libraries_path = find_libraries()
spice_library = SpiceLibrary(libraries_path)
circuit = Circuit('Diode DC Curve')
circuit.include(spice_library['1N4148'])
# 1N5919B: 5.6 V, 3.0 W Zener Diode Voltage Regulator
circuit.include(spice_library['d1n5919brl'])
circuit.V('input', 'in', circuit.gnd, 10@u_V)
circuit.R(1, 'in', 'out', 1@u_Ω) # not required for simulation
# circuit.X('D1', '1N4148', 'out', circuit.gnd)
circuit.X('DZ1', 'd1n5919brl', 'out', circuit.gnd)
simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.dc(Vinput=slice(-10, 2, .05)) # 10mV
figure = plt.figure(1, (20, 10))
zener_part = analysis.out <= -5.4@u_V
# compute derivate
# fit linear part
axe = plt.subplot(121)
axe.grid()
# Fixme: scale
axe.plot(analysis.out, -analysis.Vinput*1000)
axe.axvline(x=0, color='black')
axe.axvline(x=-5.6, color='red')
axe.axvline(x=1, color='red')
axe.legend(('Diode curve',), loc=(.1,.8))
axe.set_xlabel('Voltage [V]')
axe.set_ylabel('Current [mA]')
axe = plt.subplot(122)
axe.grid()
# Fixme:
# U = RI R = U/I
dynamic_resistance = np.diff(-analysis.out) / np.diff(analysis.Vinput)
# axe.plot(analysis.out[:-1], dynamic_resistance/1000)
axe.semilogy(analysis.out[10:-1], dynamic_resistance[10:], basey=10)
axe.axvline(x=0, color='black')
axe.axvline(x=-5.6, color='red')
axe.legend(('Dynamic Resistance',), loc=(.1,.8))
axe.set_xlabel('Voltage [V]')
axe.set_ylabel('Dynamic Resistance [Ohm]')
# coefficients = np.polyfit(analysis.out[zener_part], dynamic_resistance[zener_part], deg=1)
# x = np.array((min(analysis.out[zener_part]), max(analysis.out[zener_part])))
# y = coefficients[0]*x + coefficients[1]
# axe.semilogy(x, y, 'red')
plt.tight_layout()
plt.show()