#r# ============
#r# RLC Filter
#r# ============
#r# This example illustrates RLC Filters.
####################################################################################################
import math
import numpy as np
import matplotlib.pyplot as plt
####################################################################################################
import PySpice.Logging.Logging as Logging
logger = Logging.setup_logging()
####################################################################################################
from PySpice.Plot.BodeDiagram import bode_diagram
from PySpice import Circuit, Simulator
from PySpice.Unit import *
####################################################################################################
#r# We define four low-pass RLC filters with the following factor of quality: .5, 1, 2 and 4.
#f# circuit_macros('low-pass-rlc-filter.m4')
circuit1 = Circuit('Four double-pole Low-Pass RLC Filter')
inductance = 10@u_mH
capacitance = 1@u_uF
circuit1.SinusoidalVoltageSource('input', 'in', circuit1.gnd, amplitude=1@u_V)
#?# pulse 0 5 10 ms
# Q = .5
circuit1.R(1, 'in', 1, 200@u_Ω)
circuit1.L(1, 1, 'out5', inductance)
circuit1.C(1, 'out5', circuit1.gnd, capacitance)
# Q = 1
circuit1.R(2, 'in', 2, 100@u_Ω)
circuit1.L(2, 2, 'out1', inductance)
circuit1.C(2, 'out1', circuit1.gnd, capacitance)
# Q = 2
circuit1.R(3, 'in', 3, 50@u_Ω)
circuit1.L(3, 3, 'out2', inductance)
circuit1.C(3, 'out2', circuit1.gnd, capacitance)
# Q = 4
R4 = circuit1.R(4, 'in', 4, 25@u_Ω)
circuit1.L(4, 4, 'out4', inductance)
circuit1.C(4, 'out4', circuit1.gnd, capacitance)
#r# We perform an AC analysis.
simulator = Simulator.factory()
simulation1 = simulator.simulation(circuit1, temperature=25, nominal_temperature=25)
analysis1 = simulation1.ac(start_frequency=100@u_Hz, stop_frequency=10@u_kHz, number_of_points=100, variation='dec')
#r# The resonant frequency is given by
#r#
#r# .. math::
#r#
#r# f_0 = 2 \pi \omega_0 = \frac{1}{2 \pi \sqrt{L C}}
#r#
#r# and the factor of quality by
#r#
#r# .. math::
#r#
#r# Q = \frac{1}{R} \sqrt{\frac{L}{C}} = \frac{1}{RC \omega_0}
#r#
resonant_frequency = 1 / (2 * math.pi * math.sqrt(inductance * capacitance))
quality_factor = 1 / R4.resistance * math.sqrt(inductance / capacitance)
print("Resonant frequency = {:.1f} Hz".format(resonant_frequency))
print("Factor of quality = {:.1f}".format(quality_factor))
#o#
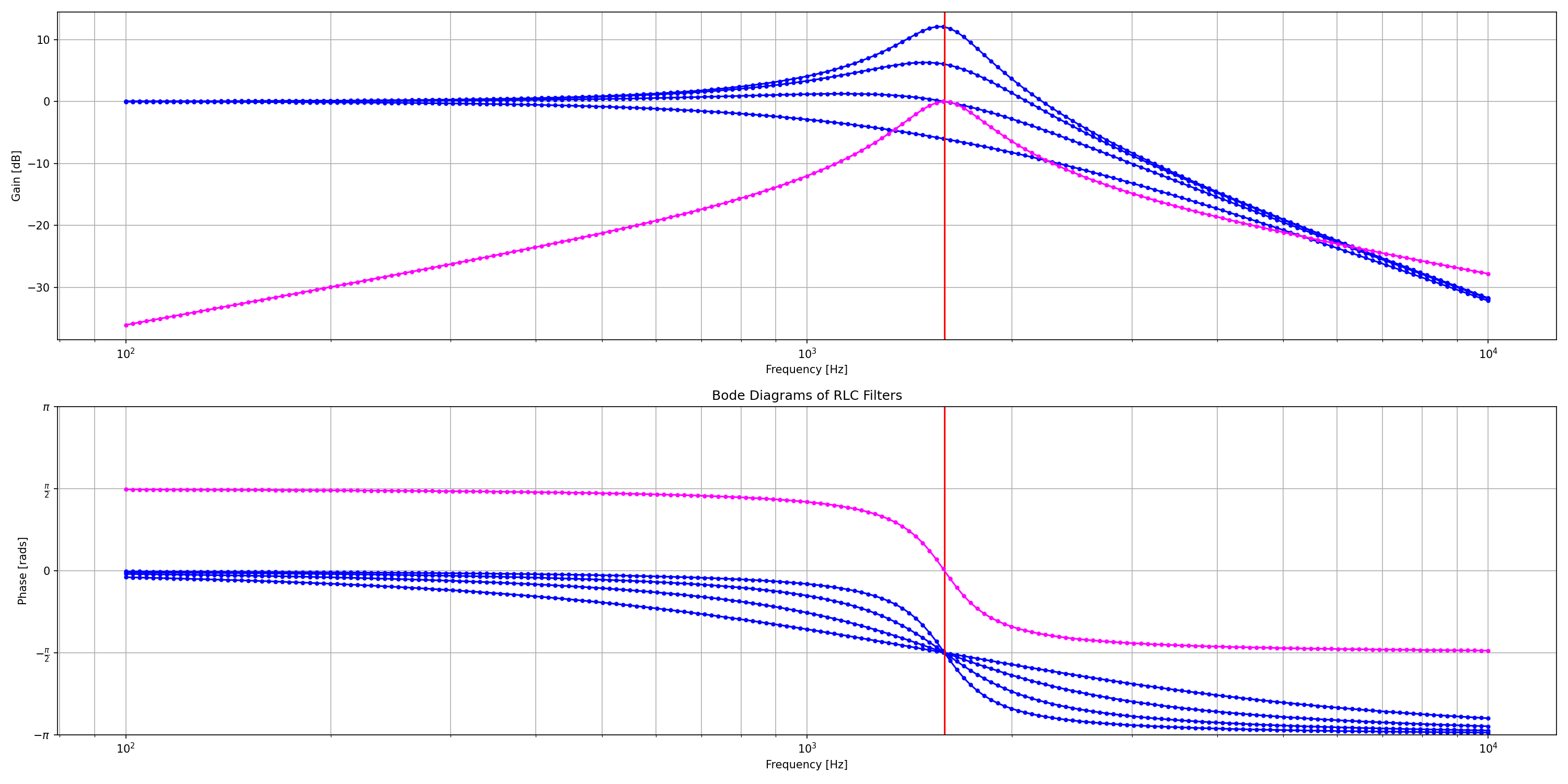
#r# We plot the Bode diagram of the four filters.
figure, axes = plt.subplots(2, figsize=(20, 10))
plt.title("Bode Diagrams of RLC Filters")
for out in ('out5', 'out1', 'out2', 'out4'):
bode_diagram(axes=axes,
frequency=analysis1.frequency,
gain=20*np.log10(np.absolute(analysis1[out])),
phase=np.angle(analysis1[out], deg=False),
marker='.',
color='blue',
linestyle='-',
)
for axe in axes:
axe.axvline(x=resonant_frequency, color='red')
####################################################################################################
#r# We define a pass-band RLC filter with a quality's factor of 4.
#f# circuit_macros('pass-band-rlc-filter.m4')
circuit2 = Circuit('Pass-Band RLC Filter')
circuit2.SinusoidalVoltageSource('input', 'in', circuit2.gnd, amplitude=1@u_V)
circuit2.L(1, 'in', 2, inductance)
circuit2.C(1, 2, 'out', capacitance)
circuit2.R(1, 'out', circuit2.gnd, 25@u_Ω)
simulation2 = simulator.simulation(circuit2, temperature=25, nominal_temperature=25)
analysis2 = simulation2.ac(start_frequency=100@u_Hz, stop_frequency=10@u_kHz, number_of_points=100, variation='dec')
bode_diagram(axes=axes,
frequency=analysis2.frequency,
gain=20*np.log10(np.absolute(analysis2.out)),
phase=np.angle(analysis2.out, deg=False),
marker='.',
color='magenta',
linestyle='-',
)
plt.tight_layout()
plt.show()
#f# save_figure('figure', 'rlc-filter-bode-diagram.png')
8.6.2. RLC Filter¶
This example illustrates RLC Filters.
import math
import numpy as np
import matplotlib.pyplot as plt
import PySpice.Logging.Logging as Logging
logger = Logging.setup_logging()
from PySpice.Plot.BodeDiagram import bode_diagram
from PySpice import Circuit, Simulator
from PySpice.Unit import *
We define four low-pass RLC filters with the following factor of quality: .5, 1, 2 and 4.
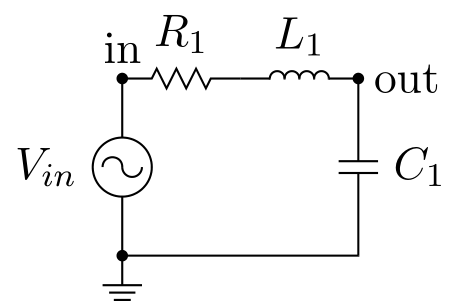
circuit1 = Circuit('Four double-pole Low-Pass RLC Filter')
inductance = 10@u_mH
capacitance = 1@u_uF
circuit1.SinusoidalVoltageSource('input', 'in', circuit1.gnd, amplitude=1@u_V)
# Q = .5
circuit1.R(1, 'in', 1, 200@u_Ω)
circuit1.L(1, 1, 'out5', inductance)
circuit1.C(1, 'out5', circuit1.gnd, capacitance)
# Q = 1
circuit1.R(2, 'in', 2, 100@u_Ω)
circuit1.L(2, 2, 'out1', inductance)
circuit1.C(2, 'out1', circuit1.gnd, capacitance)
# Q = 2
circuit1.R(3, 'in', 3, 50@u_Ω)
circuit1.L(3, 3, 'out2', inductance)
circuit1.C(3, 'out2', circuit1.gnd, capacitance)
# Q = 4
R4 = circuit1.R(4, 'in', 4, 25@u_Ω)
circuit1.L(4, 4, 'out4', inductance)
circuit1.C(4, 'out4', circuit1.gnd, capacitance)
We perform an AC analysis.
simulator = Simulator.factory()
simulation1 = simulator.simulation(circuit1, temperature=25, nominal_temperature=25)
analysis1 = simulation1.ac(start_frequency=100@u_Hz, stop_frequency=10@u_kHz, number_of_points=100, variation='dec')
The resonant frequency is given by
\[f_0 = 2 \pi \omega_0 = \frac{1}{2 \pi \sqrt{L C}}\]
and the factor of quality by
\[Q = \frac{1}{R} \sqrt{\frac{L}{C}} = \frac{1}{RC \omega_0}\]
resonant_frequency = 1 / (2 * math.pi * math.sqrt(inductance * capacitance))
quality_factor = 1 / R4.resistance * math.sqrt(inductance / capacitance)
print("Resonant frequency = {:.1f} Hz".format(resonant_frequency))
print("Factor of quality = {:.1f}".format(quality_factor))
Resonant frequency = 1591.5 Hz
Factor of quality = 4.0
We plot the Bode diagram of the four filters.
figure, axes = plt.subplots(2, figsize=(20, 10))
plt.title("Bode Diagrams of RLC Filters")
for out in ('out5', 'out1', 'out2', 'out4'):
bode_diagram(axes=axes,
frequency=analysis1.frequency,
gain=20*np.log10(np.absolute(analysis1[out])),
phase=np.angle(analysis1[out], deg=False),
marker='.',
color='blue',
linestyle='-',
)
for axe in axes:
axe.axvline(x=resonant_frequency, color='red')
We define a pass-band RLC filter with a quality’s factor of 4.
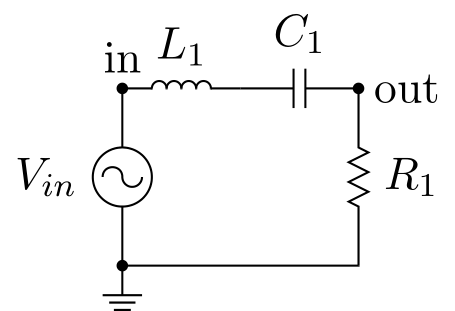
circuit2 = Circuit('Pass-Band RLC Filter')
circuit2.SinusoidalVoltageSource('input', 'in', circuit2.gnd, amplitude=1@u_V)
circuit2.L(1, 'in', 2, inductance)
circuit2.C(1, 2, 'out', capacitance)
circuit2.R(1, 'out', circuit2.gnd, 25@u_Ω)
simulation2 = simulator.simulation(circuit2, temperature=25, nominal_temperature=25)
analysis2 = simulation2.ac(start_frequency=100@u_Hz, stop_frequency=10@u_kHz, number_of_points=100, variation='dec')
bode_diagram(axes=axes,
frequency=analysis2.frequency,
gain=20*np.log10(np.absolute(analysis2.out)),
phase=np.angle(analysis2.out, deg=False),
marker='.',
color='magenta',
linestyle='-',
)
plt.tight_layout()
plt.show()